Чи пов’язані числа з природними процесами? А що спільного між мушлею равлика, бабкою та бджолами? Відповіді на ці питання шукали з Катериною Терлецькою — популяризаторкою математики, докторкою фізико-математичних наук та завідувачкою лабораторії математичних наук Малої академії наук. 

Хто такий Фібоначчі?

Справжнє ім’я Фібоначчі — Леонардо Пізанський. Це італійський математик, що жив у XII–XIII століттях. Науковець навчався у Північній Африці та багато подорожував разом із батьком-дипломатом. Після повернення до рідного міста, Пізи, створював праці з математики, а пізніше розв’язував практичні математичні задачі на замовлення імператора Фрідріха II. 

Що таке числа Фібоначчі?

Числа Фібоначчі — це послідовність натуральних чисел, тобто тих, що використовуємо при лічбі, у якій кожен наступний член є сумою двох попередніх: 1, 1, 2, 3, 5, 8, 13, 21… Катерина Терлецька стверджує: цей числовий ряд демонструє закон розвитку і зростання живих організмів. 

Цей закон ілюструє задача Леонардо Пізанського про розмноження кроликів. За умовою задачі, потрібно вирахувати, скільки пар кроликів матимемо кожного місяця, якщо одна пара щомісяця народжує двійко, які стають плідними з другого місяця життя. На початку задачі маємо двох новонароджених кроликів. Тоді за місяць усе ще буде лише одна пара, за два вони дадуть потомство й матимемо дві пари, ще за місяць — три (адже батьківська пара народить двійко, а їхні діти ще ні). Ще за місяць потомство дадуть обидві пари, що в сумі становитиме п’ять, і так далі за аналогією.

Пояснюючи цю задачу, Катерина Терлецька зауважує, що та зазнає критики біологів: науковці кажуть, що кролики розмножуються інакше. У реальному житті кролиці досягають статевої зрілості у 3,5–4 місяці, а популяцію обмежують різні чинники. Тож задача Фібоначчі не відображає дійсний біологічний процес, це лише абстрактна математична модель для ілюстрації математичних закономірностей.

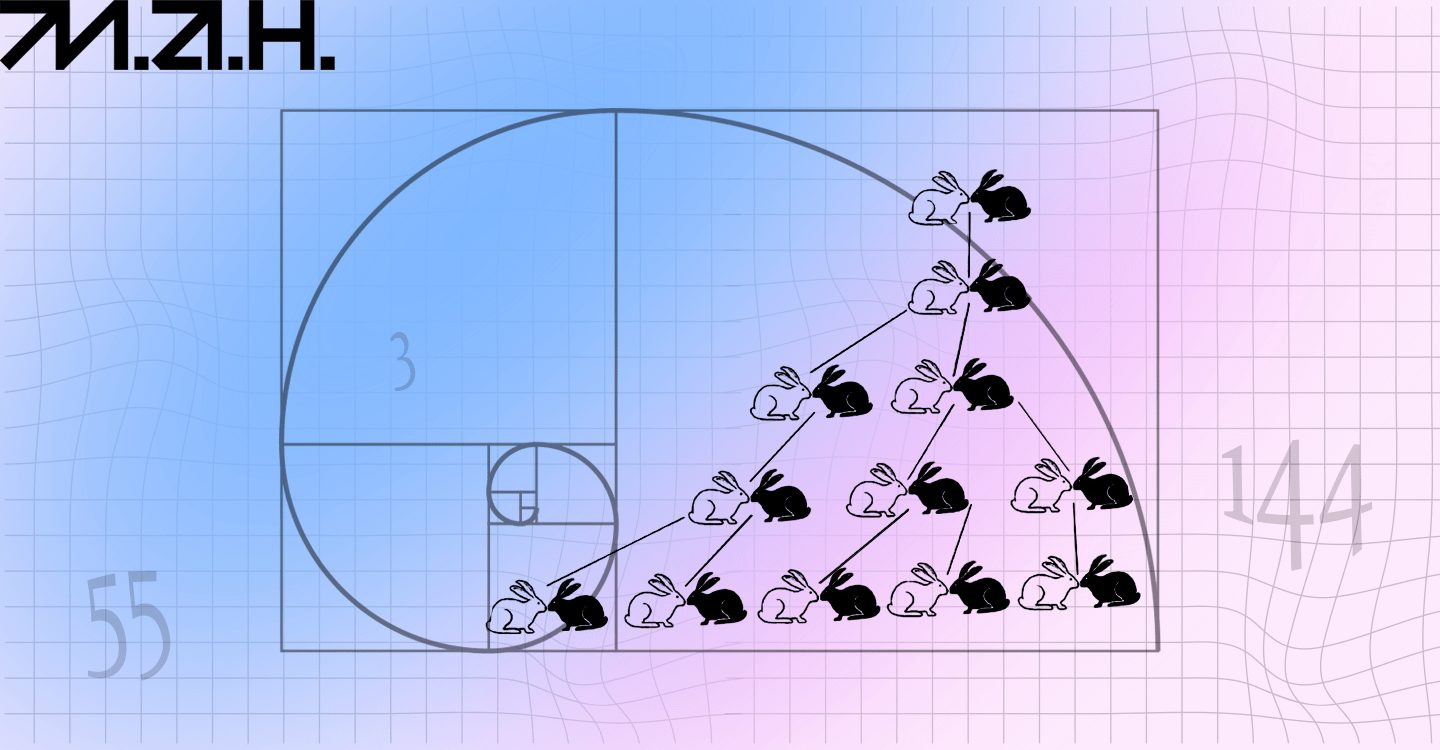
Розв’язок задачі Леонардо Пізанського про розмноження кроликів

Джерело: сайт Федеральної вищої технічної школи Цюриха

Числа Фібоначчі й золотий перетин

Золотий перетин демонструє відношення величин. Катерина Терлецька пояснює: якщо ми поділимо відрізок так, що відношення більшої його частини до меншої дорівнюватиме відношенню цілого відрізка до більшої частини, — отримаємо золотий перетин. 

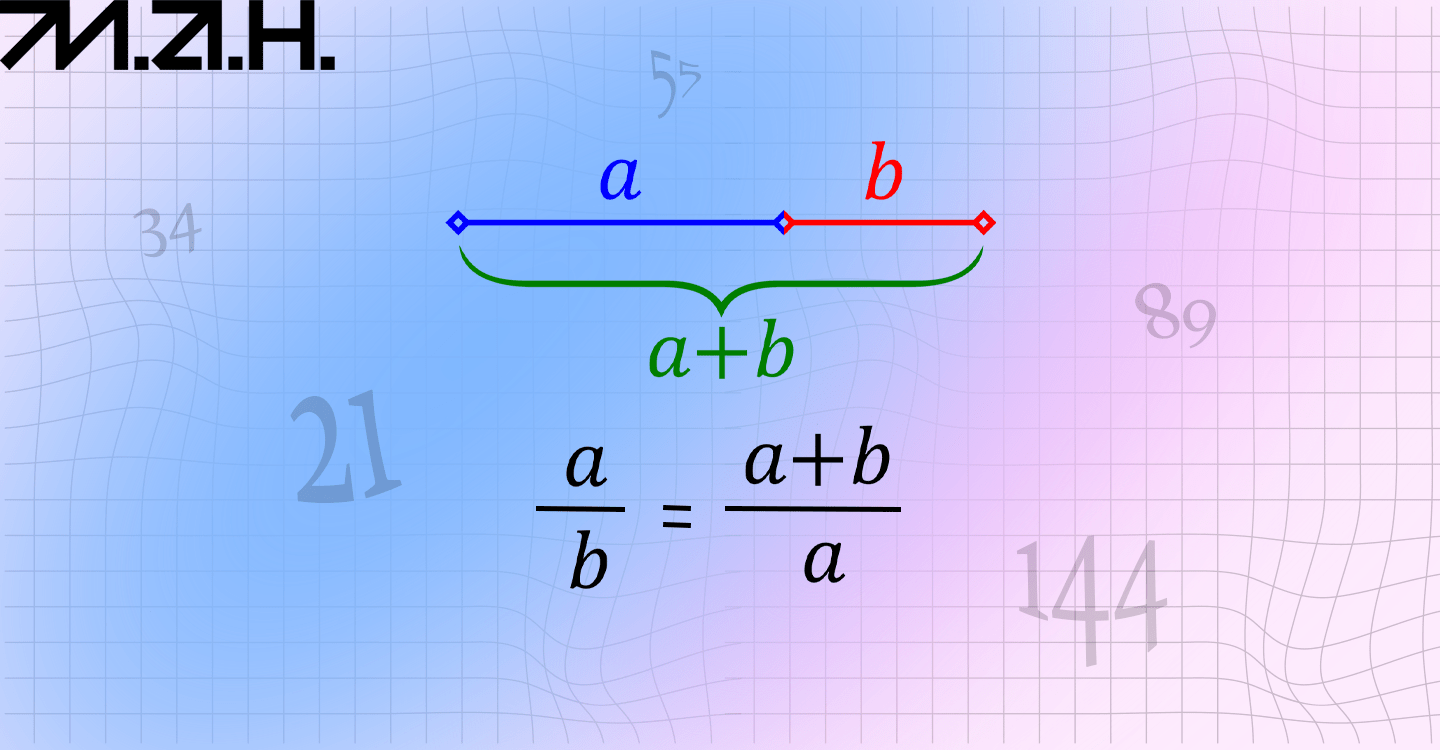
Золотий перетин

Джерело: презентація Катерини Терлецької

Замінивши у цій рівності ab на літеру фі — φ, отримаємо квадратне рівняння φ2-φ -1=0. Його додатний розв’язок — 1,618. Це число ще називають числом фі. 

Таку закономірність бачимо й серед послідовності Фібоначчі: чим далі ми рухаємося числовим рядом, тим більше відношення двох сусідніх членів наближатиметься до значення числа фі. Катерина Терлецька зауважує: хоч золотий перетин уважають ідеалом і математики, і митці, людському оку видаються приємнішими та красивішими інші відношення.

Візуалізувати це математичне поняття можна, побудувавши прямокутник з квадратів, сторони яких — послідовні члени ряду Фібоначчі. Якщо з’єднати протилежні кути цих прямокутників чвертю кола, отримаємо спіраль Фібоначчі. 

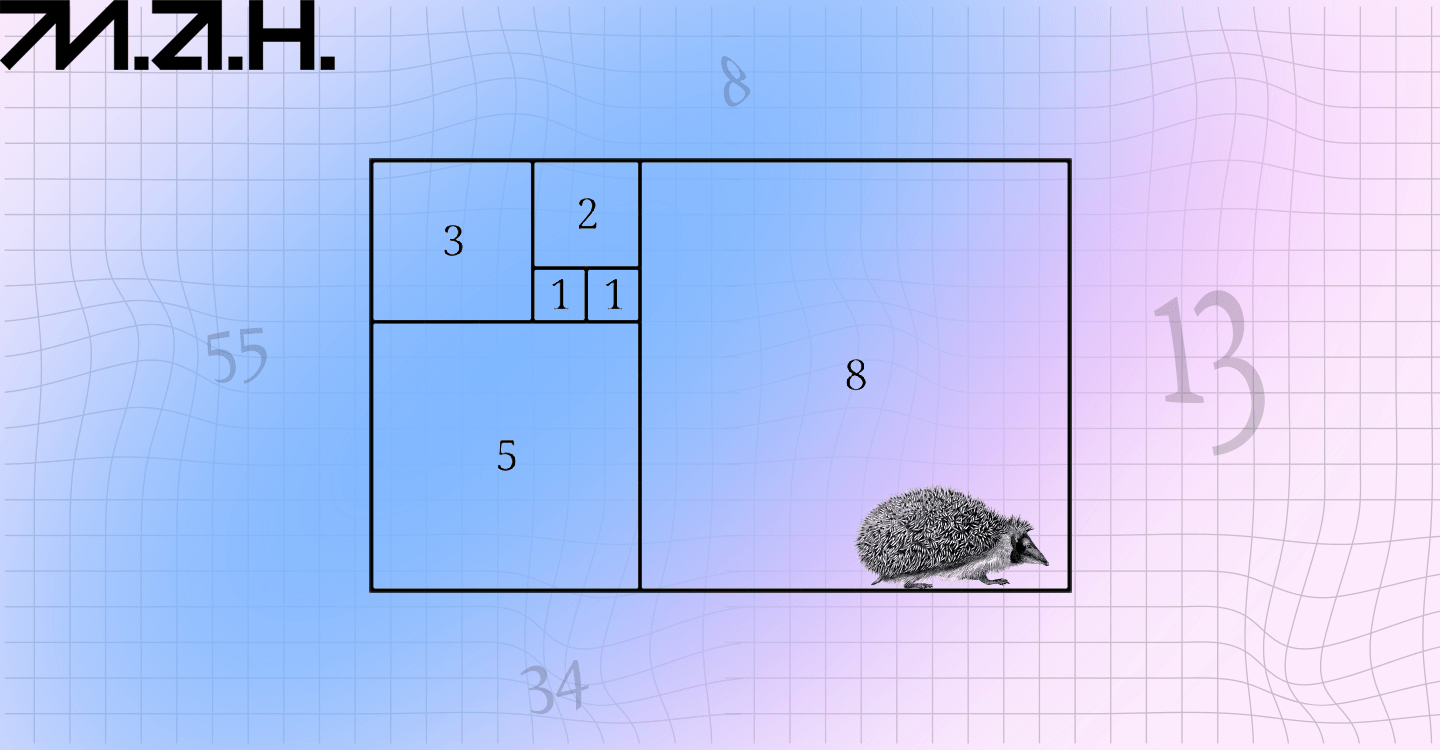
Прямокутник із квадратів, сторони яких — послідовні члени ряду Фібоначчі

Джерело: «Wikimedia Commons»

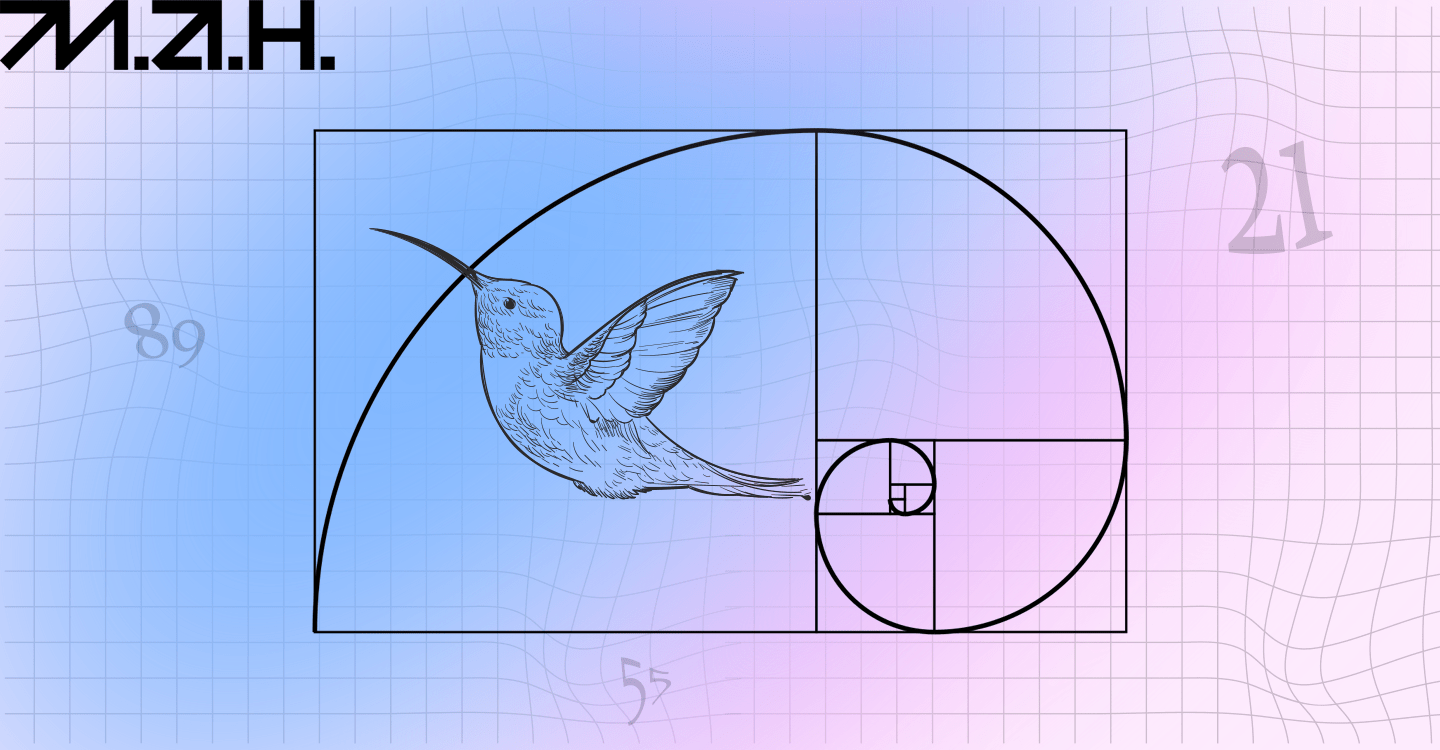
Спіраль Фібоначчі

Джерело: «Wikimedia Commons»

Вчена додає, що цей об’єкт захоплює та надихає математиків, філософів, а також архітекторів та художників. Його можемо побачити і в природі. А в журналі «The Fibonacci Quarterly» публікують математичні дослідження, пов’язані з числами Фібоначчі.

Де в природі можемо натрапити на числа Фібоначчі 

«Слід розуміти: не все, що візуально нагадує спіраль, — відображення чисел Фібоначчі. Адже спіралі бувають дуже різні, — наголошує математикиня. — От, скажімо, морська хвиля. Вона надзвичайно красива та схожа на спіраль. Проте має зовсім інший алгоритм утворення, і числа Фібоначчі ніяк його не стосуються». 

Дослідниця зауважує, що вияв математичних закономірностей у світі природи не завжди працює точно. Адже живі організми не розвиваються у вакуумі й можуть зазнавати впливу навколишніх чинників, як-от надлишок чи нестача сонячного проміння або ж поживних речовин. Через це рослини чи тварини можуть бути не такими «ідеальними», як передбачено математичною моделлю. 

На противагу морській хвилі Катерина Терлецька наводить приклад мушлі равлика. Її форма — спіраль Фібоначчі: завиток розвивається та пропорційно збільшується, зберігаючи гармонію форми.

Числа Фібоначчі часто проявляються серед квітів. Цей феномен — результат природної оптимізації, що виявляється в рослинах у вигляді симетрії, пропорцій та впорядкованості. Деякі види мають відповідну кількість пелюсток: в ірису чи лілії — по 3, у фіалок — 5. Також закономірність можна помітити на серцевині квітки. Наприклад, в ехінацеї вона складається з двох різнобічних спіралей, які ніби накладені одна на одну. Кількість завитків спіралі зазвичай збігається із числами Фібоначчі. Таку ж серцевину має квітка соняшника. 

А роздивитися золотий перетин можемо в тілі бабки. Відношення довжини її хвоста до корпусу таке ж, як відношення хвоста до довжини всього тіла. 

Катерина Терлецька зауважує: хоч задача Леонардо Пізанського про розмноження кроликів не працює на практиці, ця закономірність таки існує серед бджіл. 

У кожному бджолиному вулику є матка, яка відкладає яйця. З незапліднених яйцеклітин вилуплюється самець, трутень, із запліднених — робоча бджола. Тож у трутня є лише одна мама — матка, у неї ж — двоє батьків. Отже, трутень має бабусю та дідуся. У бабусі теж двоє батьків, тоді як у дідуся — лише батько. Таким чином, у нашого трутня троє прабатьків і так далі. 

Також є закономірність між кількістю жіночих та чоловічих особин у вулику. Відношення між ними буде числом фі — 1,618.

Числа Фібоначчі та закон росту в природі — це результат еволюційної оптимізації, яка забезпечує гармонійний розвиток і ефективне використання ресурсів.

Дізнавайся більше математичних цікавинок із МАНмедіа:

«Кола і трикутники: 5 “математичних” картин»;

«Від Панаса Мирного до Брема Стокера: письменники, які захоплювалися математикою»;

«Math-life balance: які хобі мали відомі математики».

Ілюстрації: Олена Ковальчук